Temps de lecture : 10 minutes
Netmath a pour mission d’aider chaque élève à découvrir et développer son propre potentiel mathématique avec plaisir.
Simon, technopédagogue et expert Netmath, vous propose dans « Simon se demande » d’aborder avec vos élèves une question du quotidien d’un point de vue des mathématiques. Une façon pour eux de se rendre compte que les maths peuvent être vraiment le fun lorsqu’il s’agit de mieux comprendre le monde qui les entoure.
Aujourd’hui, Simon se demande quel est l’intérêt d’être sympa avec son voisin et même l’impact que ça peut avoir sur la société en général. Ici, notre réflexion nous amènera à aborder les notions de calcul de l’aire d’une figure, la représentation d’un nombre ainsi que la construction d’un arbre de possibilités.

Être sympa avec son voisin, ça peut s’appliquer à des situations du quotidien presque anecdotiques comme tenir la porte à la personne qui suit ou laisser sa place à une personne âgée dans les transports en commun, mais aussi à des situations plus engageantes… comme partager une information.
Pour comprendre ce qui est en jeu ici, je vais prendre un exemple concret. Imaginons que trois élèves, Carl, Claire et Clarence, doivent résoudre un problème mathématique.
On y observe trois merveilleuses façons d’arriver à un même résultat! Par contre, Claire, Carl et Clarence, n’ont accès qu’à une seule solution … la leur. C’est malheureux puisque comme on le voit d’un point de vue extérieur, chaque idée est différente des autres. Chaque exploration a quelque chose de particulier.
Imaginons maintenant qu’ils décident de réfléchir ensemble. Qu’arrive-t-il?
Et bien, au terme de leur réflexion, chaque élève aura exploré 3 façons différentes de résoudre un même problème mathématique. D’abord, je constate que les élèves sont confrontés à 3 fois plus d’idées mathématiques. La leur, plus celle des 2 autres élèves ce qui donne effectivement 3 idées.
Tout fonctionne!
Mais je ne pense que ça pourrait aller encore plus loin! Un élève pourrait être inspiré par le travail d’un autre!!!
OK imaginons par exemple que toutes les premières idées inspirent les autres à générer une nouvelle idée! Quelle serait la répercussion sur le nombre total d’explorations mathématiques?
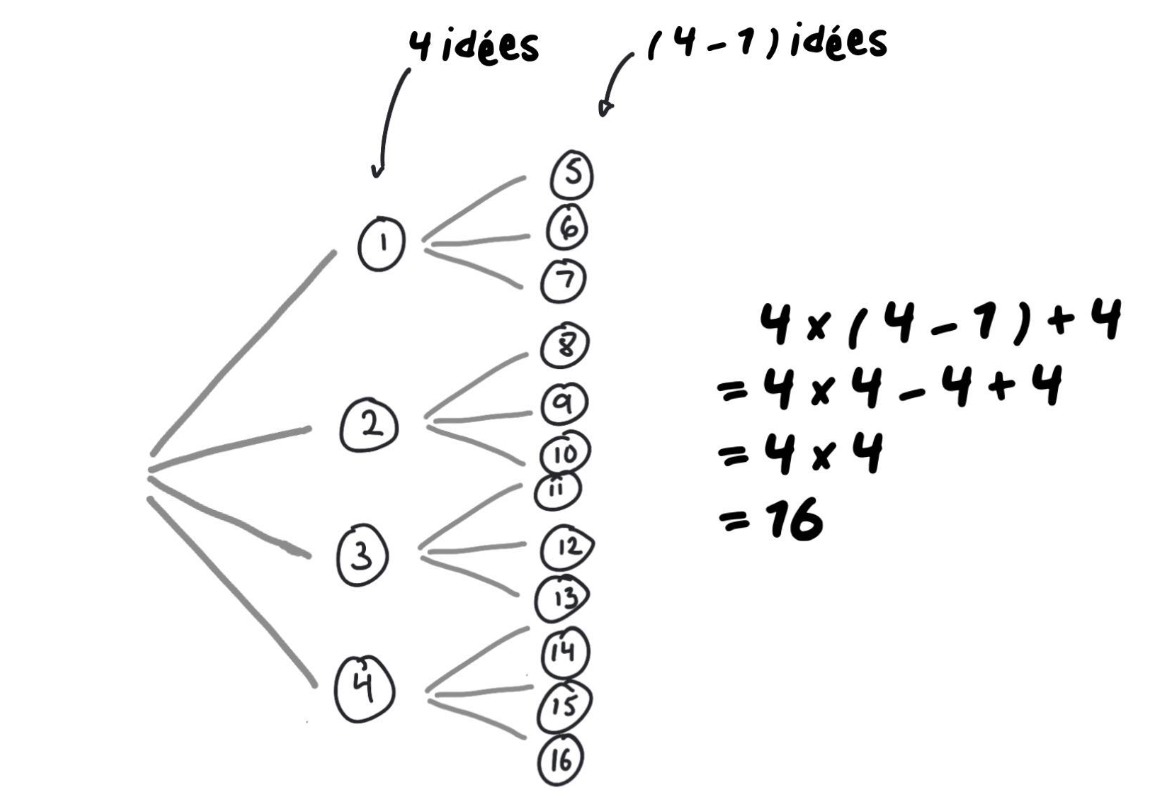
Je pense que le meilleur moyen de répondre à cette question serait de faire un arbre des possibilités avec toutes les idées des élèves!
On voit donc qu’on a 3 idées au départ et que ça donne lieu à la génération de 6 nouvelles propositions … pour un total de 3 + 6 = 9 solutions au problème!
Fait intéressant : 3 x 3 est également égal à 9 ! Il y a avait 3 élèves et on a un total de 9 idées!
Est-ce que ça veut dire que pour 4 élèves on aurait 4 x 4 = 16 idées?
On dirait bien que oui! On dirait même que si on a n élèves on va avoir n x n idées!
Donc pour une classe de 30 élèves ça donne … Woow 900 idées!
Ça peut faire peur qu’autant d’idées surgissent mais faisons confiance à l’intelligence collective. Après la phase de divergence vient toujours la phase de convergence où l’enseignant a un rôle clé à jouer!
En résumé, l’ouverture aux idées extérieures permet de voir les situations de manières différentes. Et comme le souligne Jo Boaler, auteure de Mathematical Mindset, cette exposition aux réflexions variées vient nettement enrichir la qualité de l’apprentissage #mentalitédecroissance!
Pour l’année à venir, souhaitons-nous donc d’avoir l’occasion de partager davantage nos idées et d’apprendre des autres.
Alors, n’oubliez pas de partager cet article et revoyez les concepts en jeu avec votre classe sur Netmath!